平行
薬剤学研究室 中村 任 教授
真っ直ぐに延びた線路、どこまでも続く線路、その先にはどんな光景が待っているのでしょうか。今すぐにでも日常を忘れて旅に出たくなります。

ところで、線路に使用されている2本のレールは平行に並んでいるため交わることはありませんが、写真の中のレールは遠くに行くほど狭くなり、いずれ交わるように見えます。ここで「平行」について少し考えてみたいと思います。「平行」を辞書で引くと次のように説明されています。
【平行】(出典:大辞林)
- 同一平面上の二直線が交わらないこと。また、空間の直線と平面、あるいは平面と平面が交わらないこと。また、そのさま。
- 「並行」に同じ。
- 意見などがいつまでも一致しないこと。
今、直方体を紙面に描こうとすると図1や図2のような書き方が思いつきます。
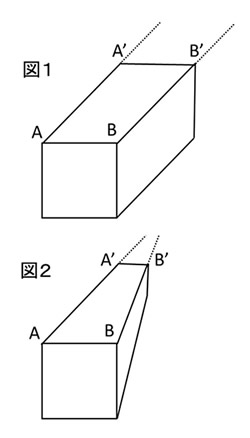
等角投影法や一点透視図法などと呼ばれていた気がします。直方体上の線分AA’と線分BB’に着目すると、2点A、A’を通る直線とB、B’を通る直線は同一平面上で平行の関係にあるため、両者が交わることはありません(図1)。他方、図2においても2点A、A’を通る直線とB、B’を通る直線は同一平面上では平行関係にあるのですが、図面上で見ると両直線はいずれ交わることになります。一点透視図法は肉眼やカメラのレンズを通して見ると遠くのものが小さく見えることを利用した図法であり、ある一点で消失(収束)するように描かれているため2本の平行線がいずれ交わることは当たり前ともいえます。ただ、反対に考えてみると、描き方や認識の仕方によって平行でない2本の直線に対して平行関係や奥行きを持たせたりすることができる点で大変興味深いです。
今度は、球面上で考えてみます。球面上に直線を引こうとすると任意の2点を通り球面に沿って最短で結ぶ線を引くことになりますが、その線は球の中心を通る平面によって球を切り取ってできる断面の円に相当します(図3)。したがって、球面上に引いた2本の線(円)は球面上のいずれか2点で交わることになり、同一球面上では平行関係にある2本の線を描けないことになります。
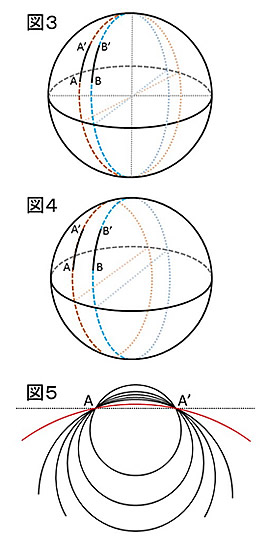
図4のように2本の直線を球面上で交差しないように引けるような気もしますが、この場合は線分AA’が球面上で最短とはなりません。図5を見れば分かりますが、2点A、A’を球面上(曲線上)に最短で結ぼうとした場合、2点は球面上に描ける最大の円周上にきますから、結局、図3のようになります。メルカトル図法で描かれた世界地図の各経線は平行ですが、地球儀で見るといずれの経線も北極と南極で交わることを思い浮かべるとわかりやすいかもしれませんね。
「平面上」や「球面上」、「最短で結ぶ」などの前提条件は物事の見方や捉え方を決定する上で大変重要なことです。時に話し合いなどをしていると、話が平行線をたどったり、同じ話を繰り返したり、そもそも何を話し合っていたのかさえ分からなくなったりすることもあります。そんな時は、一度原点に立ち戻って前提条件を整理すれば、平行線をたどる議論も最短でま~るく収束させることができるかもしれませんね。
(終)
参考:
【直線】(出典:大辞林)
まっすぐな線。二点を結ぶ最短の線。
【曲線】(出典:大辞林)
まがった線。直線でない線。数学では、直線も曲線の特別な場合とみることがある。カーブ。


